Quantifying intratumor heterogeneity in cancer

Introduction

Researchers working on cancer evolution often want to address questions related to intratumor heterogeneity. Given that a patient’s cancer isn’t a homogeneous disease, but is instead composed of genetically heterogeneous cells, we often want to compare heterogeneity between different conditions. This can mean comparing heterogeneity at different timepoints—for instance, one project I contributed to required comparing heterogeneity for colorectal cancers before and after treatment. The hypothesis driving the project was that treatment would select for cell subpopulations able to resist the therapy, with vulnerable subpopulations dying and reducing the cancer’s heterogeneity. Once treatment stopped, heterogeneity would increase again in the absence of the selective pressure. In other instances, we can imagine comparing cancer samples from a tumour’s primary site and a metastasis, with the intent to determine whether the seeding event that created the metastasis and the different selection pressures in its new environment led to more or less heterogeneity relative to the primary. We can also consider applications where we compare patient groups. Suppose we spilt cancer patients into “high heterogeneity” and “low heterogeneity” groups, then followed them through time to see whether members of one group survived longer on average than members of the other. A melanoma study found that patients with more heterogeneity typically fared worse, likely because the immune response to the disease was reduced relative to patients with less heterogeneity.

All of these applications require some means of quantifying heterogeneity. Once you can measure heterogeneity numerically, you can conduct statistical hypothesis tests and start to formulate conclusions. There are, however, many ways in which you can go about quantifying heterogeneity, with two of the most prominent methods being regrettably misleading. In the sections that follow, I will show why those methods are wrong, how we can correct the most promising definition, and how we can extend the corrected definitions to incorporate additional information about cancer evolution.

A cancer evolution primer

Before delving into intratumor heterogeneity, we need to establish some baseline definitions. Cancers are not homogeneous entities within a patient, but instead consist of mixtures of genetically heterogeneous cells. Cells become cancerous because they defeat the mechanisms making the cells cooperate as part of the larger organism. Oftentimes, this happens because the cells have acquired a series of genetic mutations that cripple these mechanisms. The mutations may occur because of exposure to mutagens, such as cigarette smoke or UV light, or because of errors that accumulate through the process of cell division. Most such mutations will be inherited by all cancer cells that descend from this founding cancerous population. Critically, however, mutation acquisition does not end at the onset of disease—cells continue to acquire new mutations as they divide and the cancer grows.

This process of evolution can lead to the emergence of genetically distinct subpopulations of cells within the cancer, as some cancer cell subpopulations may have a competitive advantage relative to others. For instance, some populations may be able to escape predation by the immune system, or may acquire the capacity to leave the tumour’s site of origin and seed a metastasis elsewhere in the body. Even in the absence of selection, we expect that some populations may come to dominate through the process of neutral evolution, with earlier subpopulations having more time to grow and thus coming to represent more of the tumour. Given bulk DNA sequencing data from one or more tissue samples taken from a patient’s cancer, we can reconstruct the genetic profiles of these different subpopulations, determine what fraction of each cancer sample corresponds to each subpopulation, and infer the evolutionary history of how these subpopulations developed through time.

Methods such as my recently published Pairtree reconstruct the evolutionary history of a cancer using bulk DNA sequencing data. As input, Pairtree uses mutation read counts from one or more samples taken from a patient’s cancer. In each sample, cells from the constituent subpopulations are intermixed, and so deconvolving these into the individual subpopulations is one of the primary challenges posed by evolutionary history reconstruction. From mutation read counts, we estimate the variant allele frequency (VAF) of each mutation in each sample. By correcting for the effect of copy-number aberrations, we convert these allele fractions, reflecting what proportion of alleles in the sample carry the variant, into estimates of subclonal frequency, reflecting what proportion of cells carry the variant. We then use the subclonal frequencies across one or more cancer samples to reconstruct the disease’s evolutionary history.

Suppose we depict the evolutionary history of a cancer with the following schematic.

Figure 1: Evolutionary history of a single patient’s cancer. Each coloured blob represents a genetically distinct subpopulation of cells. We sample mixtures of these subpopulations at three different points in time, subject the samples to genomic sequencing, and recover the intermixed allele frequencies of mutations in each subpopulation.

Each coloured blob represents a genetically distinct cell subpopulation, emerging from within the mass of its parent. The founding purple cancerous subpopulation emerged from normal cells within the parent, corresponding to the beginning of the cancer’s growth. We take tissue samples from the patient at three different points in time, with two coming from the primary disease site and the third from a metastasis. Each sample contains a mixture of the different cell subpopulations present in the cancer at that point in time and space. Using the VAFs of the mutations we observe within genome sequencing data for the sample, we will produce a clone tree.

Figure 2: Clone tree depicting the evolution of the cancer given in fig. 1.

Observe that this tree maps to the disease schematic above. Each tree node represents a genetically distinct cell subpopulation. Associated with each tree node is one or more mutations that distinguish cells in that subpopulation from subpopulations ancestral to it on the tree, or subpopulations on different tree branches. Directed edges indicate evolutionary descent, with an edge from node $A$ to node $B$ showing that $B$ descended from $A$ and inherited all its mutations. Thus, a subpopulation’s genotype consists of the mutations associated with that tree node, as well as with all nodes ancestral to it (i.e., all nodes on the path through the tree from the subpopulation’s node to the tree root). A subclone corresponds to a tree node and all its descendants. For a subpopulation $A$, all subpopulations in the corresponding subclone inherit the mutations that first appeared in $A$, which we assume are not borne by any other subpopulations in the tree.

For a given clone tree, we have two associated types of frequency data.

Figure 3: Subclonal frequencies and population frequencies for the cancer depicted in fig. 1. In each sample, the subclonal frequencies match the height of the subclone in fig. 1 (blob and its descendent blobs), while the population frequencies match the height of the subpopulation (single blob alone).

In each cancer sample, each tree node has a subclonal frequency, representing what proportion of cells descended from the corresponding subpopulation. Equivalently, the subclonal frequency indicates what proportion of cells carry the mutations that first appeared in the subpopulation that initiated the subclone. In each cancer sample, we also assign a population frequency to each tree node, indicating what proportion of cells from the subpopulation compose the cancer sample. The population frequency also can be understood as indicating what proportion of cells in the cancer sample have the same genotype. (Genotype is defined only with respect to the mutations provided as input to Pairtree—cells within a subpopulation will differ with respect to other mutations, such as those not captured by the sequencing platform in use [e.g., intronic mutations for whole-exome data] or mutations too low in frequency to call from the sequencing data.) Observe that both the subclonal and population frequencies above map to the initial disease schematic. By definition, the population frequencies must sum to one in each cancer sample, since every observed cell must have originated from one of the subpopulations. The subclonal frequencies obey no such sum constraint. Instead, the subclonal frequency constraints require the tree’s root node to have a subclonal frequency of one in every sample, since every cell belongs to this subclone (i.e., the subclone corresponding to the entire tree). Additionally, given a parent node $A$ and child $B$, the subclonal frequency of $A$ must be at least as great as $B$‘s subclonal frequency in every cancer sample.

Critically, even when multiple samples are provided from the same cancer, a single clone tree describes the evolutionary history of that patient’s disease, with every sample mapping to that tree. In particular samples, some subclones or subpopulations can have frequencies of zero, indicating that the subclone or subpopulation was not present in that sample. For quantifying intratumor heterogeneity, the population frequencies will be critical.

How the data appear

Given our above definition of subclonal frequency, we can now examine the data we expect to observe. Clone tree construction, and thus intratumour heterogeneity measures, are based on the read counts we observe for the mutations we detect in one or more cancer samples. First, we will define our notation. We take the following as input.

$K$: number of subclones
$S$: number of cancer samples
$M$: number of mutations across all samples
$T_{ms}$: number of total reads at mutation $m$‘s locus in sample $s$
$V_{ms}$: number of variant reads at mutation $m$‘s locus in sample $s$
$\omega_{ms}$: probability of observing the variant allele when sampling reads from mutation $m$‘s locus in sample $s$ for a subclone carrying the mutaiton
$C_m \in \{ 1, 2, \ldots, K \}$: subclone to which mutation $m$ is assigned

The $C_m$ values correspond to a variant clustering, whereby subclone $j$ is distinguished by the variants $i$ with $C_i = j$, and all such variants are assumed to have the same allele frequencies across all cancer samples, once those frequencies have been corrected for the effect of copy-number aberrations. In addition to the tree structure, we infer the following.

$\phi_{ks}$: subclonal frequency of subclone $k$ in sample $s$
$\eta_{ks}$: population frequency of population $k$ in sample $s$

These frequencies are subject to some constraints.

$\sum_{k=1}^K \eta_{ks} = 1$ for each sample $s$
$\phi_{is} \geq \phi_{js}$ if subclone $i$ is ancestral to subclone $j$ in the tree, for each sample $s$
$\phi_{0s} = 1$ in each sample $s$, where subclone $0$ corresponds to the tree’s root node, representing normal tissue

For notational convenience, we will use $\Phi_s = [\phi_{1s}, \phi_{2s}, \ldots, \phi_{Ks}]$ to represent the $K$-dimensional vector of all subclonal frequencies from sample $s$. Likewise, we will use $\Eta = [\eta_{1s}, \eta_{2s}, \ldots, \eta_{Ks}]$ to represent the $K$-dimensional vector of all population frequencies. When we are considering single-sample datasets, we will omit the subscripts on $\Phi$ and $\Eta$.

As the tree’s root node represents normal tissue and has no assigned mutations, the tree will have $K+1$ nodes. We can now define a binomial observation model for each cancer sample $s$ such that

$$ V_{ms} \sim \text{Binom}(T_{ms}, \omega_{ms} \phi_{C_{m}s}) \ . $$

Thus, in each cancer sample $s$, our mutation frequency data will appear as a mixture of $K$ binomials, with the mixture proportions depending on how many mutations are assigned to each subclone. Suppose we have a three-subclone tree built from a single cancer sample. (We omit the root node 0 from the tree rendering to improve clarity.)

Figure 4: Example three-subclone linear tree.

We inferred this tree from the following VAF data for $M = 10,000$ mutations, which will be the same value of $M$ we use throughout this post.

Figure 5: VAF data corresponding to tree in fig. 4.

This VAF data was sampled from three binomials mixed with proportions $Z = [0.28, 0.44, 0.28]$. We used the subclonal frequencies $\Phi = [\phi_{1,1}, \phi_{2,1}, \phi_{3,1}] = [0.65, 0.40, 0.25]$ and a constant read depth $T = 275$. To make the visualizations more aesthetically pleasing and the data easier to reason about, we set $\omega_{ms} = 1$ for all mutations across all samples; in the typical diploid autosomal case for humans with a locus unaffected by copy-number aberrations, we would have $\omega_{ms} = \frac{1}{2}$, but this difference does not affect our conclusions.

Before moving on to heterogeneity measures, we must define purity, since we use it in the next section. The purity of a cancer sample indicates what proportion of cells are cancerous. In typical trees that have a single founding cancerous cell subpopulation, the purity is equal to the largest subclonal frequency (excluding the tree root that represents non-cancerous cells), which would be $65\%$ in the tree above.

Sometimes the MATH doesn’t work out

The Mutant Allele Tumour Heterogeneity (MATH) score is a widely used method of quantifying tumour heterogeneity, whose popularity is evident from the many recent cancer papers using MATH scores. The MATH score was first defined in 2013, with its continued popularity perhaps stemming from the easily accessible implementation of MATH scores in the R package maftools. For a single cancer sample $s$, MATH is defined with respect to the VAF distribution, such that

$$ \text{MATH}(s) = \frac{\text{MAD}(s)}{\text{median}(s)} \ , $$

where $\text{MAD}(s)$ represents the median absolute deviation of the VAFs in the sample, while $\text{median}(s)$ provides the median. The intuition for MATH is straightforward: more variance in your VAF distribution suggests more subclones are present in your cancer sample, and so it’s more heterogenous. MATH’s simplicity is appealing—we needn’t impose any structure on the data, such as a clone tree or even variant clusters, to compute MATH.

At first blush, the MATH performs as we would hope. Let’s return to the three-subclone VAF distribution from above. Recall this was generated with subclonal frequencies $\Phi = [0.65, 0.40, 0.25]$, read depth $T=275$, and mixture proportions $Z = [0.28, 0.44, 0.28]$.

Figure 6: VAF data corresponding to tree in fig. 4. The MATH score for this data is 0.333.

If we compute the MATH for this VAF distribution, we get $0.333$. Suppose now we generate a two-subclone dataset with $\Phi = [0.65, 0.45]$, $T=275$, and $Z = [0.65, 0.35]$.

Figure 7: VAF data for tree with two subclones. The MATH score for this data is 0.107.

For this dataset, the MATH is only $0.107$, and so we correctly conclude that this cancer sample has less heterogeneity. MATH appears to work. MATH’s limitations become clear, however, when we consider that the score is defined with respect to two simple summary statistics about the VAF distribution. Many VAF distributions can have similar summary statistics and thus similar MATH scores despite originating from cancers with vastly different amounts of heterogeneity. Consider the following VAF distribution, sampled for two subclones with $\Phi = [0.59, 0.3]$, $Z = [0.5, 0.5]$, and $T=100$.

Figure 8: VAF data for another tree with two subclones. The MATH score here is 0.333.

The MATH here is $0.333$, just as with our first VAF distribution—in fact, the two MATHs differ by only $1.11 \times 10^{-16}$. (To find the parameters for a binomial mixture that had the same MATH as the first example, I used academia’s favourite optimization algorithm, which is highly parallelizable and extremely cost efficient: Grad Student Search. Specifically, I fiddled with the subclonal frequencies and read depth until the MATH score was close to my desired value, then randomly sampled point sets until the MATH had a tiny divergence from my target.) By manipulating the subclonal frequencies, mixture proportions, and read depths, we maintained a nearly constant MATH score despite losing an entire subclone and reducing the cancer sample’s heterogeneity. Once we decide to play VAF distribution games, we can formulate even starker examples. Suppose we generate data for a cancer with only a single subclone, using $\Phi = [0.2]$ and $T = 15$.

Figure 9: VAF data for a single-subclone tree. The MATH score here is again 0.333.

Though the MAD and median change substantially, the MATH established from their ratio is very nearly constant at $0.333$. This is alarming—this cancer sample has no heterogeneity, as it corresponds to only a single subclone, yet has the same MATH as datasets with two and three subclones.

If we really want to have fun with summary statistics, we can define an algorithm for radically changing a VAF distribution while maintaining a constant MATH score. Specifically, we can select an arbitrary point in an existing VAF distribution, then move the point while keeping the MAD and median constant, thereby maintaining the MATH. In moving this point, we must obey two constraints:

To maintain the median, the point must stay on the same side of the median. That is, if it’s currently less than the median, it must remain so.
To maintain the MAD, the point’s absolute deviation from the median must stay on the same side of the MAD. That is, if the point’s absolute deviation from median is greater than the MAD, it must remain so.

The combination of these two constraints yields four cases, each of which defines a subset of the unit interval over which our chosen point can be moved while maintaining the distribution’s MAD and median. Julia code I wrote to perform these point-swapping modifications is available on GitHub. If we begin with our original three-subclone VAF distribution, then apply this point-moving operation $100,000$ times, we end up with this distribution.

Figure 10: VAF data with MATH score of 0.333. To generate this data, we began with the original VAF distribution from fig. 6, then randomly relocated points using the uniform distribution.

This distribution is radically different from the original VAF distribution, yet has the same median and MAD, which yield the same MATH of $0.333$. To produce the modified distribution, in each point-moving iteration, the algorithm sampled the selected point’s new location uniformly from the interval that maintained the distribution’s summary statistics. But we need not sample the new location uniformly, as the following modified distribution makes clear.

$VAF data with MATH score of 0.333. To generate this data, we began with the original VAF distribution from fig. 6, then randomly relocated points using the $\textit{Beta}(5,5)$ distribution.$

Figure 11: VAF data with MATH score of 0.333. To generate this data, we began with the original VAF distribution from fig. 6, then randomly relocated points using the $\textit{Beta}(5,5)$ distribution.

Again, we maintain the same median and MAD to produce a MATH of $0.333$. In this case, each time we needed to move a point within its constrained interval, we sampled the new location from a $\text{Beta}(5,5)$ distribution, then applied a linear transformation to keep the point within the required interval. While the uniformly sampled case we examined previously yields a VAF distribution unlike one we would ever expect to observe in real data, the distribution here is more realistic. Note the four distinct VAF clusters—applying this operation resulted in an additional cluster appearing, without any effort on our part to produce this effect. Given the locations of the largest bins in each cluster, this data could have been generated by four subclones with $\Phi = [0.14, 0.33, 0.48, 0.78]$.

$VAF data with MATH score of 0.333. To generate this data, we began with the original VAF distribution from fig. 6, then randomly relocated points using the $\textit{Beta}(\frac{1}{2},5)$ distribution.$

Figure 12: VAF data with MATH score of 0.333. To generate this data, we began with the original VAF distribution from fig. 6, then randomly relocated points using the $\textit{Beta}(\frac{1}{2},5)$ distribution.

Similarly, we can begin with our original three-subclone VAF distribution and generate a much different distribution using a $\text{Beta}(\frac{1}{2},5)$ followed by the linear transformation to sample each point’s destination on its constrained interval. Here we see four distinct VAF clusters with long tails to the right of each cluster. Each cluster’s tail can be thought of as arising from neutral evolution, with selective sweeps producing the four distinct clusters followed by periods with minimal selection. Once more, visualizing the VAF distribution reveals information about evolution and heterogeneity not captured by the MATH score.

We can thus condemn MATH as having too little relation to the heterogeneity that it purports to measure. VAF distributions with vastly different amounts of heterogeneity can yield the same MATH score. MATH’s shortcomings arise from a simple problem: the MATH scores tries to summarize complex information with two simple summary statistics. As I discuss in the Conclusion section, all metrics that characterize complex phenomena will be subject to this problem to varying degrees. MATH, however, does not impose sufficient structure on the data to capture enough information about heterogeneity so as to make itself useful.

Before moving on from MATH, we will address one final question: why does the score divide by the VAF distribution median, instead of using the MAD alone? In the supplement for the paper that first defined MATH, the authors note that they divide by the median VAF in an attempt to correct for the effect of varying sample purities, so that MATH scores can be compared between cancer samples. They correctly note that dividing mutation VAFs by the sample purity will convert the VAFs from proportions of all alleles, to proportions of only cancer alleles. However, because they don’t compute the purity, they try to approximate it with the VAF distribution’s median. This need not, however, have any relation to sample purity—we expect sample purity to be well approximated by the VAF median only when more mutations arose in the founding subclone (i.e., the one with the highest subclonal frequency) than in the rest of the subclones combined. There is no reason to expect this condition to hold for most cancers, and, indeed, in most analyses of real data I’ve done, it does not.

SDI: translated from ecology to cancer, but not quite right

The Shannon diversity index (SDI) is well-established in ecology, where it is defined simply as the Shannon entropy of the proportions of populations in an ecosystem, with those population proportions composing a discrete probability distribution. Some uses of the SDI normalize it to lie on the unit interval—given $K$ populations, the maximum entropy will be $\log_2 K$, corresponding to the entropy of the uniform probability distribution with $K$ components, and so we can divide the SDI by this value to normalize it. This concept has an obvious application to cancer heterogeneity studies, where each subclone corresponds to a separate population. The aforementioned Wolf et al. (2019) melanoma study claimed to use SDI to compare heterogeneity between patients.

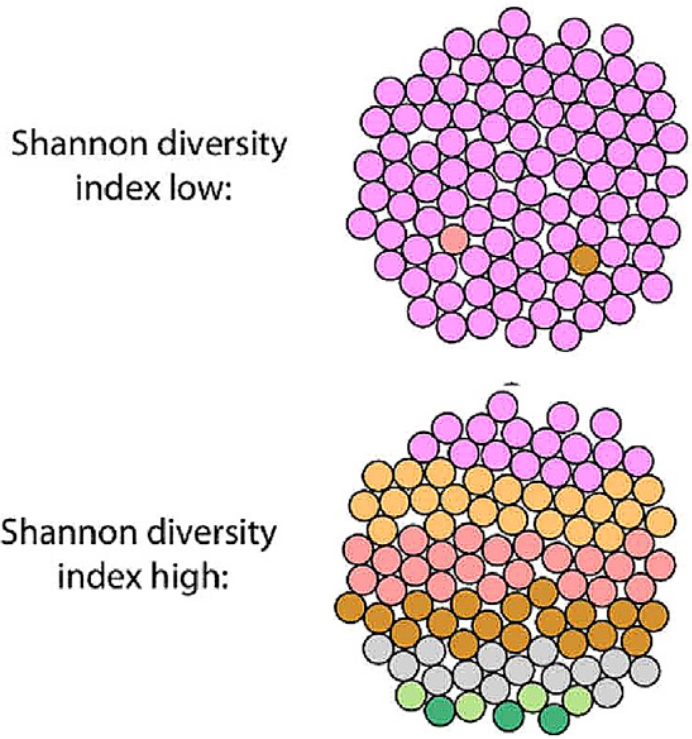
Figure 13: The Shannon diversity index (SDI) as defined schematically by Wolf et al. (2019) (taken from fig. 7A).

The paper defines SDI schematically in a sensible fashion (fig. 13), as each small circle represents a cancer cell coloured according to the subclone from which it originated. If this definition were accurate, it would be an accurate translation of the SDI into the cancer heterogeneity domain. Unfortunately, the paper’s supplement reveals that the authors actually defined SDI with respect to the fraction of total mutations borne by each mutation cluster, with each cluster assumed to correspond to a distinct subclone. Specifically, given $M$ total mutations in a patient, we define $|M_k|$ to be the fraction of mutations in cluster $k$, such that

$$ |M_k| = \frac{\sum_{m=1}^M \bm{1}_{C_m = k}}{M} \ . $$

Then we define the SDI for cancer sample $s$ as the entropy of the discrete probability distribution composed of these fractions, so that

$$ \text{SDI}(s) = -\sum_{k=1}^K |M_k| \log_2 |M_k| \ . $$

This definition, unfortunately, is inconsistent with how SDI is used in ecology. We would expect SDI to be based on the prevalence of different cell subpopulations composing the cancer. SDI as defined here, however, is based solely on the proportion of mutations assigned to each subclone, which is conceptually unrelated to the ecology definition. In the following section, I will consider how we can restore the correct definition of SDI, which I will refer to as the clone diversity index (CDI) to avoid confusion with the Wolf et al. (2019) SDI definition.

Wolf et al. (2019) uses SDI to characterize heterogeneity for patients in four previously published immune checkpoint inhibitor cohorts, in an attempt to provide support for their own melanoma analyses that suggest more subclones and more mutational diversity lead to worse clinical outcomes. The authors used previously published mutation clusters from PyClone for three of the cohorts, and defined their own clusters for patients in the fourth cohort using the CHAT algorithm. For each patient, the authors computed the SDI of the mutation clusters. They then split each of the four patient cohorts into “high SDI” and “low SDI” groups using the median SDIs from each, going on to show that the “high SDI” groups had worse survival. Though the results are convincing, given significant differences in survival between the groups in each cohort, the methodology is not—there is no reason to suspect that a more equitable distribution of mutations amongst subclones should lead to worse outcomes. We might expect that a measure incorporating tumour mutation burden (TMB), which refers to how many mutations a cancerous subpopulation carries, would be informative, as more mutations present more potential neoantigens for the immune system to attack. Past studies have shown that higher TMB in a cancer as a whole is (loosely) correlated with worse survival. The SDI, however, looks only at how equitably mutations are divided between subclones, not the absolute numbers of mutations. Moreover, the SDI doesn’t even tell us about the relative number of mutations that are carried by each cancerous cell subpopulation composing the cancer. As discussed above, each subpopulation inherits all the mutations of its ancestral subpopulations, and so without placing the subpopulations and subclones in a tree structure, we have no idea what the mutation burdens borne by those subpopulations are, and thus no notion of their potential immunogenicity.

The greatest weakness of SDI comes from how it does not incorporate population frequencies. Suppose, for instance, that a patient’s cancer sample was composed of two subpopulations of cells. Intuitively, if the population frequencies were equally split such that each population composed $50\%$ of cells, we would want to say that the cancer is more diverse than if the frequencies were split such that one population corresponded to $90\%$ of cells and other to $10\%$ of cells. In the latter case, if we were to sample a single cancer cell from the tumour, we could be fairly certain it came from the $90\%$ population; in the former case, we would have considerably more uncertainty about which population gave rise to our selected cell. The SDI does not capture this.

Given the significant differences in patient survival between high-SDI and low-SDI groups, what is the underlying mechanism driving these results? I suspect the predictive power of the authors’ improperly defined SDI can be explained by how it captures aspects of the proper CDI definition, given how mutations are observed and clustered.

There is a one-to-one relationship between clusters, subclones, and cell subpopulations, and so increasing the number of mutation clusters will generally increase both the SDI and CDI. Thus, because there is one subpopulation for every mutation cluster, more mutation clusters will generally lead to a higher SDI (ignoring how equitably mutations are divided amongst those clusters), and also lead to a higher CDI (ignoring how equitably the population frequencies in that sample are divided amongst the subpopulations).
Each mutation cluster must have a corresponding subpopulation with non-negligible population frequency, and so will increase the CDI. If the associated subpopulation had negligible population frequency, it would have nearly the same subclonal frequency as its parent, and thus be impossible to discern when clustering mutations. Inherently, more mutation clusters will lead to a higher SDI; the fact we can identify more clusters implies each must have non-negligible population frequency, and so will also increase the CDI.

Consequently, SDI captures some of the same information as the proper definition provided by the CDI, but this is purely coincidental. Given their mutation clusters, the authors could have built clone trees, computed subclonal frequencies and population frequencies, and reported a diversity measure based on population frequencies. They did not, presumably, because this would have required considerably more investment in the analysis of these data, for what was only a secondary result in their paper.

Before moving on from SDI, we should note one possible interpretation of the SDI. Assuming positive selection occurs in a series of selective sweeps through a cancer’s evolutionary history, the proportion of mutations borne by a subclone can tell us something about how much time passed between selective sweeps, since a subset of mutations accumulates at a relatively steady rate through a clock-like process. Additionally, because we can identify a subclone as distinct from its descendants, we know the sweep was not complete because it left some cells from the parental subpopulation intact. Thus, SDI may reflect how many selective sweeps have occurred, and the relative length of time intervals between them. Higher SDIs would reflect more sweeps, with more balanced time periods between them. This signal, however, is likely weak, as many factors can confound the clock-like properties of these mutational processes, and positive selection need not have occurred. Caution must thus be used with this SDI interpretation.

CDI: establishing the correct definition of the SDI

Translating the ecology definition of SDI to cancer genomics is straightforward—as a diversity index, it should reflect how many distinct cell subpopulations exist in a cancer sample, and the relative abundances of each. To avoid confusion with the improper definition of SDI given by Wolf et al. (2019), I will refer to the corrected definition as the clone diversity index (CDI). Because a cancer sample’s subpopulation frequencies sum to one, they can be understood as a categorical probability distribution over subpopulations. These subpopulation frequencies only sum to one, however, when the non-cancerous founding population $0$ is included, such that for a cancer sample $s$, we have $\sum_{k = 0}^K \eta_{ks} = 1 \ .$ As we want to exclude this non-cancerous population when characterizing cancer heterogeneity, we define re-normalized, cancer-specific subpopulation frequencies $\tilde{\eta}_{ks} = \frac{\eta_{ks}}{\sum_{k = 1}^K \eta_{ks}} \ .$ The CDI is then defined for a cancer sample $s$ as

$$ \text{CDI}(s) = -\sum_{k=1}^K \tilde{\eta}_{ks} \log_2 \tilde{\eta}_{ks} \ . $$

Thus, the CDI is simply the Shannon entropy of the frequencies of the subpopulations composing the cancer sample. Intuitively, the CDI reflects how uncertain an experimenter would be in subpopulation identity if she selected a cancer cell at random from a cancer sample, with higher CDI values reflecting that a cancer sample is composed of a more diverse mixture of subpopulations. The maximum CDI of $\log_2 K$ is reached when all subpopulations are present in a cancer sample in equal proportions. Other cancer studies have put the CDI to good use. Noble et al. (2020) also recognized that clonal heterogeneity should be quantified with respect to population frequencies, where they use the inverse Simpson index rather than the Shannon entropy to quantify the diversity represented by those frequencies. Although the Shannon entropy and inverse Simpson index have different mathematical definitions, they are essentially interchangable with regard to interpretation. Likewise, Maley et al. (2017) enumerated different means of quantifying diversity for their Evo-index, including using the Shannon entropy and inverse Simpson index with population frequencies. In addition, Carvagna et al. (2018) defined the SDI for determining the heterogeneity of cancer evolutionary trajectories (see section 2.2 in the Carvagna et al. (2018) supplement).

Some subpopulations can have zero subpopulation frequencies. Practically, this occurs when the mutation clustering is defined using subclonal frequencies across multiple cancer samples, and a subpopulation cannot be discerned from its parent in one sample (where it has the same subclonal frequency as its parent), but it can be separated in one or more other samples. Though $\log_2 0 = -\infty$, we have $\lim_{a \rightarrow 0} a \log_2 a = 0$, so we define $0 \log_2 0 = 0$. Thus, there is no problem mathematically, though some care must be taken computationally to avoid computing $0 \log_2 0$, as this will usually produce a warning or error from your numerical computing library about computing the logarithm of zero.

We realize several benefits with this corrected definition.

The CDI allows easy comparisons of diversity between multiple samples from the same cancer. Suppose we had samples taken from a patient at diagnosis and later at disease relapse, and wanted to test the hypothesis that relapse samples were less diverse than diagnosis samples, on the assumption that treatment selected for subpopulations able to resist treatment while eliminating vulnerable subpopulations. We can simply compute the CDI for each sample and compare them to test this notion. The SDI, conversely, is poorly suited for this task because, when working with multiple cancer samples, the same mutation clusters should be shared across samples, so that two mutations appear in different clusters if their estimated subclonal frequencies are substantially different in one or more cancer samples. We can attempt to overcome this deficiency of the SDI by clustering mutations separately in each sample, but the structure this imposes on the data maps poorly to the underlying biological truth. We should use the richest representations our data permit, which require using the cancer samples jointly to cluster mutations.
The CDI can capture information about subpopulation diversity that is not driven by genetic factors. Suppose a population’s expansion is driven by epigenetic or transcriptomic selective advantages not reflected in bulk DNA sequencing data. The frequency of that population will be reflected in the prevalence of its constituent mutations, even if those mutations did not cause its expansion, and so CDI can give us insight into population heterogeneity without assuming it was caused by genetic factors. To some extent, the SDI as given in Wolf et al. (2019) can do the same, but only because it captures some of the same information as the CDI, as described in the SDI section above. The CDI is clearer and more explicit as to how it represents heterogeneity, even when that heterogeneity is not created through selection on genetic mutations.

In using the CDI, we must consider a fundamental ambiguity that often arises in clone tree problems.

$Example three-subclone linear tree with subclonal frequencies $\Phi = [0.65, 0.45, 0.20]$, population frequencies $\Eta = [0.2, 0.25, 0.2]$, and a CDI of $1.43$.$

Figure 14: Example three-subclone linear tree with subclonal frequencies $\Phi = [0.65, 0.45, 0.20]$, population frequencies $\Eta = [0.2, 0.25, 0.2]$, and a CDI of $1.43$.

$Example three-subclone branched tree with subclonal frequencies $\Phi = [0.65, 0.45, 0.20]$, population frequencies $\Eta = [0, 0.45, 0.2]$, and a CDI of $0.98$.$

Figure 15: Example three-subclone branched tree with subclonal frequencies $\Phi = [0.65, 0.45, 0.20]$, population frequencies $\Eta = [0, 0.45, 0.2]$, and a CDI of $0.98$.

Both of the above trees are defined from the same subclonal frequencies, obtained from the estimates given in the same VAF data, yet have different structures that impose different subpopulation frequencies and thus different CDIs. Even with noise-free knowledge of the subclonal frequencies, it is impossible to distinguish which tree is correct given these data. Typically, we require multiple cancer samples to determine which tree likely corresponds to the truth. Any heterogeneity analyses must account for this ambiguity, which the SDI as given in Wolf et al. (2019) does not.

CMDI, CADI: Incorporating tree structure and mutation burden into diversity measures

With the correct definition of the Shannon diversity index restored through the CDI, we consider two extensions. The first is the clone and mutation diversity index (CMDI), which incorporates information about the TMB, reflecting how many mutations are borne by each clone. This is distinct from the SDI, which uses the proportion of mutations borne by each clone, not the mutation counts.

In a clone tree, every subpopulation $k$ has a mutation cluster representing mutations that arose on the evolutionary path between $k$ and its parent. All descendants of $k$ inherit its mutations. Thus, the full set of mutations $M_k$ possessed by a subpopulation $k$ consists of its mutations and the mutations of its ancestors, defined as $M_k = \{ m | C_m = k \lor C_m \text{ is an ancestor of } k \text{ in the clone tree} \}.$ Here we use the same $M_k$ notation as in our SDI definition above, but define it as representing the union of mutation clusters dependent on $k$‘s position in the tree structure, rather than the lone mutation cluster associated with $k$. For each $M_k$ mutation set, we create a conditional discrete uniform distribution $p(m | k)$, such that $p(m | k) = \frac{1}{ |M_k| } ,$ where $|M_k|$ represents the number of mutations in the associated set. From this, we create a joint distribution over subpopulations $k$ and mutations $m$ so that $p(k, m) = p(m | k) p(k)$. Each such joint distribution is specific to a cancer sample $s$ because the distribution over subpopulations $p(k)$ is defined by the population frequencies in that sample. Thus, the subpopulation distribution should be denoted $p_s(k) = \tilde{\eta}_{ks}$, but we omit the subscript on $p(k)$ for notational convenience. The CMDI is then the joint entropy of $p(k, m)$, so that

$$ \begin{align*} \text{CMDI}(s) &= -\sum_k \sum_m p(k,m) \log_2 p(k,m) \\ &= -\sum_k \sum_m p(m | k) p(k) \log_2 (p(m | k) p(k)) \\ &= -\sum_k p(k) \Big[ \sum_m p(m | k) \log_2 p(k) + \sum_m p(m | k) \log_2 p(m | k) \Big] \\ &= -\sum_k p(k) \Big[ \log_2 p(k) + \sum_m p(m | k) \log_2 p(m | k) \Big] \\ &= -\sum_k p(k) \log_2 p(k) + p(k) \sum_m \frac{1}{|M_k|} \log_2 \frac{1}{|M_k|} \\ &= -\sum_k p(k) (\log_2 p(k) - \log_2 |M_k|) \\ &= -\sum_k \tilde{\eta}_{ks} (\log_2 \tilde{\eta}_{ks} - \log_2 |M_k|) \ . \end{align*} $$

The CMDI reflects how uncertain an experimenter would be in subpopulation and mutation identity if she selected a cancer cell at random from a cancer sample, then selected a mutation at random from the cell’s associated subpopulation. Higher CMDI values reflect that a cancer sample is composed of a more diverse mixture of subpopulations, and/or that the subpopulations composing it bear a higher mutation load. This higher mutation load may occur because the subpopulations themselves have many mutations that occurred on the evolutionary path from their parents to them, or because the subpopulations occur deep within the clone tree such that they have many ancestors whose mutations they inherited.

We can use the ideas underlying the CMDI to develop a similar index named the clone and ancestor diversity index (CADI). Intuitively, the CADI reflects how much uncertainty you have if you sample a cancer cell according to a cancer sample’s population frequencies, then uniformly sample an ancestor population of that cell. Higher CADI values indicate a sample is composed of a more diverse mixture of subpopulations, and/or that the prevalent subpopulations have more distinguishable ancestors, reflecting a protracted evolutionary process. The CADI achieves this in a similar way to the CMDI—while CMDI used a discrete uniform distribution over mutations $p(m|k)$, the CADI uses a discrete uniform distribution over ancestors $p(a|k)$. If subpopulation $k$ has $A_k$ ancestral populations in the clone tree, we define $p(a|k) = \frac{1}{|A_k|}$. The derivation of the CADI for cancer sample $s$ is then nearly the same as the expression for CMDI, yielding

$$ \begin{align*} \text{CADI}(s) &= -\sum_k \sum_a p(k,a) \log_2 p(k,a) \\ &= -\sum_k \tilde{\eta}_{ks} (\log_2 \tilde{\eta}_{ks} - \log_2 |A_k|) \ . \end{align*} $$

We could combine these ideas to create a joint distribution over populations, mutations, and ancestors $p(k,m,a) = p(k) p(m|k) p(a|k)$ and compute the entropy of this to produce another index, but it’s not clear it would offer much additional utility.

Applying the diversity indices and characterizing uncertainty

My clone tree reconstruction method Pairtree implements the CDI, CMDI, and CADI. We will illustrate these metrics by running Pairtree on one of the acute lymphoblastic leukemia cancer datasets published in Dobson et al. (2020), using patient SJMLL026. Throughout this analysis, we will focus on characterizing uncertainty in our results. This dataset has 73 cancer samples, allowing us to define eight subclones from 25 mutations. First, we will examine the tree with the highest posterior probability, along with its population and subclonal frequencies, and the consensus graph depicting uncertainty in tree structure.

Figure 16: Highest posterior probability clone tree built with Pairtree for patient SJMLL026 from Dobson et al. (2020). Tree nodes are coloured to show lineage prevalence at time of diagnosis (blue) and relapse (red).

Figure 17: Population frequencies for highest-posterior tree built with Pairtree for SJMLL026 from Dobson et al. (2020). The CDI and CMDI values rendered here are normalized to the highest observed value across cancer samples for each index, so that each value lies on the unit interval.

Figure 18: Subclonal frequencies for highest-posterior tree built with Pairtree for SJMLL026 from Dobson et al. (2020).

The tree’s subclones are coloured according to subclonal frequency at time of diagnosis (blue) and at relapse (red), showing that two subclones (7 and 8) were specific to diagnosis, while the branch with subclone 2 at its head was specific to relapse. In the frequency plots, we show the frequencies of one cancer sample per column. “Diagnosis” and “Relapse” correspond to patient tissue samples from these timepoints, while the dXeno and rXeno samples correspond to mouse xenografts at diagnosis and relapse, respectively. Xenograft tissues were taken from bone marrow (“BM”) or the central nervous system (“CNS”). We show only a subset of the 73 cancer samples here to simplify the visualizations. The population frequency plot shows CDI and CMDI values for this tree, normalized to the largest CDI or CMDI observed across samples. These results reflect only the single tree with the highest posterior mass.

Because there is uncertainty in the tree structure, we must expand our analysis to incorporate this.

Figure 19: Consensus graph built with Pairtree for SJMLL026 from Dobson et al. (2020).

The consensus graph represents all possible parent-child relationships observed across trees that exceed a given posterior threshold. Here, the minimum spanning-tree threshold is $56\%$, reflecting that the least-certain parent relationship in the dataset can be resolved with $56\%$ confidence. This reflects two credible tree candidates. The more probable tree, given $55\%$ posterior weight, has population 6 rendered as the parent of population 4, while the less probable tree, with $44\%$ posterior weight, reverses this relationship. (The other $1\%$ of posterior mass is assigned to a medley of less credible trees.) We achieve near-certainty in the other parts of the tree only because we have so many cancer samples; most datasets will have more uncertainty than seen here in their tree structure.

For illustrative purposes, the uncertainty in tree structure observed here is helpful, as it allows us to consider the effect of this uncertainty on our diversity indices. We can now examine the CDIs, CMDIs, and CADIs for this dataset.

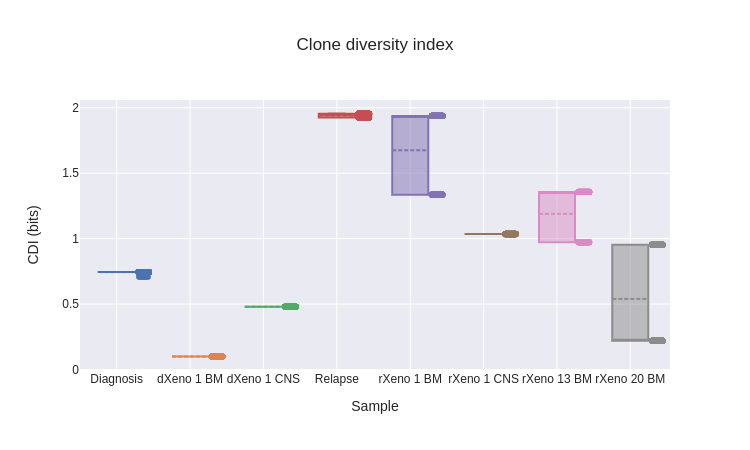
Figure 20: CDIs for each cancer sample in SJMLL026 from Dobson et al. (2020).

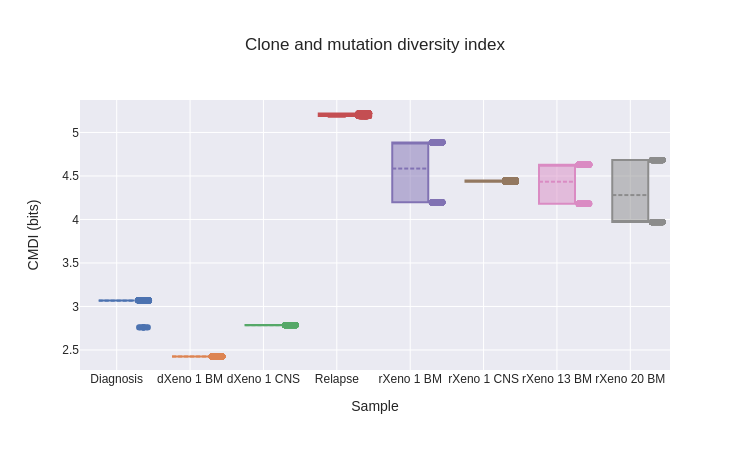
Figure 21: CMDIs for each cancer sample in SJMLL026 from Dobson et al. (2020).

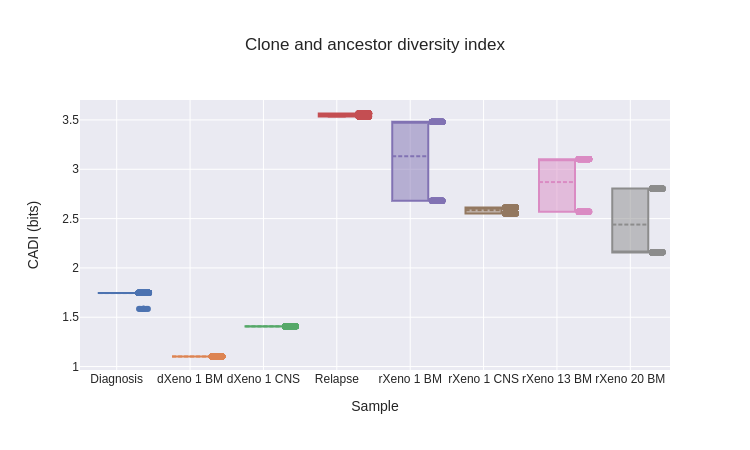
Figure 22: CADIs for each cancer sample in SJMLL026 from Dobson et al. (2020).

As defined, the three diversity indices produce a single scalar value for each cancer sample. To characterize uncertainty in the diversity indices, we took a bootstrapping-based approach. Using the posterior probabilities assigned to each tree, we sampled 1000 trees (with replacement) from the posterior distribution and computed the diversity indices for each. This then gave us distributions over the diversity indices for each sample. Across the diversity indices, we see three patterns.

The diversity of diagnosis samples is less than in relapse samples. This is supported by the population frequencies for the highest-probability tree (fig. 17), where we see diagnosis samples dominated by one subpopulation, while the relapse samples have a more diverse mix. In general, nearly the same ranking of samples is maintained across the three diversity indices, reflecting that they are all capturing similar information. The most substantial discrepancy between indices occurs for rXeno 20 BM, where it seems to have comparable diversity to diagnosis samples via the CDI, but greater diversity via CMDI and CADI. This difference occurs because, at least in the highest-posterior tree, this sample consists almost entirely of pop. 4 (fig. 17), which occurs deep in the tree (fig. 16) and so drives CMDI and CADI relatively higher.
Diversity of the initial patient samples (“Diagnosis” and “Relapse”) is greater than the xenografts they seeded. To some extent, this may occur because the xenografts were deliberately created with a varying number of cancer cells from the patient, spanning many orders of magnitude. Regardless of how many cells were xenografted into a particular mouse, there was only ever a subset of cells from the original sample, which likely would have represented a less diverse mixture. Additionally, since the mice were immunodeficient, and there was no consequent immune predation of the xenografted cancer, the selective environment may have favoured the emergence of fewer dominant subpopulations in each mouse.
Little uncertainty exists in the diversity indices. For this dataset, the only uncertainty in population frequencies stems from the relative positions of populations 4 and 6 in the tree, and the consequent uncertainty in those populations’ frequencies. The three diagnosis samples have almost none of this lineage (fig. 18), and so have no uncertainty in diversity indices.

Uncertainty in the tree structure produces uncertainty in the rankings of the diversity indices. To ascertain whether one cancer sample is more diverse than another, we can use a Wilcoxon signed-rank test with any of our three diversity indices. Critically, relationships between diversity indices in different tree samples are paired, since they depend on a given tree structure—a test that simply compares the distributions over diversity indices for different samples without accounting for this mutual interdependence, such as a Mann-Whitney U test, would not be appropriate.

For instance, using the CADIs from our last example (fig. 22), we can ask whether the rXeno 13 BM sample has higher CADIs than the rXeno 20 BM sample. From the box plot alone, this is not clear, as both samples produce bimodal distributions, and we could well have most posterior samples correspond to the higher mode in rXeno 20 BM and the lower mode in rXeno 13 BM, rendering rXeno 20 BM more diverse than rXeno 13 BM. However, when we do a Wilcoxon signed-rank test with the null hypothesis that rXeno 13 BM has lower CADIs than rXeno 20 BM, we obtain a result with $p = 2.19 \times 10^{-59}$, allowing us to reject the null and conclude that rXeno 13 BM is more diverse than rXeno 20 BM.

Summary and conclusion

We have shown that two published means of quantifying intratumor heterogeneity are deceiving. MATH is misleading because it is computed from two summary statistics of a cancer sample’s VAF distribution, and different VAF distributions that correspond to vastly different degrees of heterogeneity can produce the same statistics. SDI as defined in Wolf et al. (2019) is misleading because it measures how equitably mutations are distributed between subclones, which has no clear relationship to intratumor heterogeneity. For technical reasons, some correlation occurs between this measure and the proper definition of SDI from ecology (i.e., CDI as defined here), which is likely why the authors were able to demonstrate predictive value for this measure with respect to patient outcome. Despite this success, we should strive to use a measure with a clear and obvious link to the heterogeneity it purports to measure, rather than one that captures this information unintentionally.

Motivated by the deficiencies of MATH and SDI, I proposed three alternative measures.

CDI uses the proper definition of SDI from ecology, measuring how many distinct cell subpopulations exist in a patient’s cancer and how balanced they are in composing a cancer sample.
CMDI extends the CDI to incorporate information about the tumor mutation burden in the subpopulations composing a cancer sample.
CADI extends the CDI to reflect how many evolutionary steps between ancestral subclones occurred on the path to the subpopulation composition observed in a cancer sample.

To better understand the differences between diversity measures, it helps to consider the amount of structure they impose on your data.

MATH imposes no structure, simply using summary statistics to characterize the VAF distribution. Consequently, MATH can mislead—by changing properties of the generative model, such as read depth, we showed that multiple VAF distributions can have the same MATH scores despite consisting of one, two, three, or four clearly distinguishable subclones.
SDI, conversely, imposes a limited degree of structure by clustering mutations into subclones, but this structure doesn’t capture any biologically important properties.
CDI, CMDI, and CADI impose more structure by using more complex models. Conceptually, the additional model complexity is a weakness, since the data can violate assumptions made by the model, such as the infinite sites assumption, and so compromise the model’s veracity. However, this degree of structure is necessary to recover biologically relevant properties of the data. As ever, all models are wrong, but some are useful.

More generally, three lessons emerge from our attempts to quantify intratumor heterogeneity.

Summary statistics can mislead. All of these measures attempt to depict a complex picture of heterogeneity using a single number. It will always be possible for datasets with varying degrees of heterogeneity to yield similar values for such a metric. We explicitly demonstrated this weakness for MATH scores, but CDI and its brethren are not exempt.
Look at your damned data. We are visual creatures, and so a VAF histogram confers much more information about heterogeneity than a statistic like MATH that tries to summarize it. Of course, it’s still possible to game your data depictions—you can, for instance, manipulate the bin size of your histogram to tell substantially different stories about the same data. Nevertheless, the relative richness of visualizations makes them harder to game. For the MATH examples, a quick glance at the VAF histograms revealed how different the heterogeneity was between examples despite them having the same MATH scores. Even if you need a number so you can make an objective claim about something quantifiable, as we did when we used the Wilcoxon test to show that one cancer sample consistently had a higher CADI than another, you should frequently spot-check your data by visualizing it and ensuring your claims are consistent with how the data appears.
Metrics are valid only when there exists a clear, intuitive link between them and biological properties of interest. SDI lacks this connection; MATH has an intuitive link between its value and the heterogeneity it claims to measure, but fails for other reasons. CDI, CMDI, and CADI are imperfect, as any measures must be, but they succeed in establishing this intuitive connection. CDI is particularly appealing because of its simplicity—it addresses the question, “If I randomly select a cancer cell from my sample, how uncertain am I about the cell subpopulation from which it arose?” This definition has been helpful in sketching the intuition underlying the metric for collaborators with no training in statistics or information theory. Typically, this property is precisely what researchers hope to capture when assessing heterogeneity, and so it justifies the complexity of the model necessary to compute CDI, CMDI, and CADI.