A probabilistic perspective on binary classification metrics

Introduction

Precision, recall (or, synonymously, sensitivity), and specificity are ubiquitous metrics in binary classification problems. Machine learning people typically favour precision and recall, which underlie the precision-recall (PR) curve that shows how a classifier performs at different classification thresholds, illustrating the trade-off that occurs between these metrics. Conversely, people working on problems in medicine often prefer sensitivity and specificity, which yield the receiver operating characteristic (ROC) curve that captures a similar depiction of the trade-offs between the two metrics. Most definitions of the metrics first establish a confusion matrix showing that every data point can be regarded as a true positive (TP), true negative (TN), false positive (FP), or false negative (FN), and then compute the metrics using the integer counts of points in each class. However, a probabilistic perspective on precision, recall, and sensitivity is much more illuminating.

Consider a binary classification problem with predictions $\hat{y}$ and true labels $y$, with both taking the values $0$ or $1$. Our three metrics can then be defined probabilistically.

Metric	Definition
Precision	$p(y=1 \| \hat{y}=1) = \frac{TP}{TP + FP}$
Recall (or sensitivity)	$p(\hat{y}=1 \| y=1) = \frac{TP}{TP + FN}$
Specificity	$p(\hat{y}=0 \| y=0) = \frac{TN}{TN + FP}$

While defining these metrics with respect to the four confusion-matrix classes requires careful deliberation, and often trips me up when I return to binary classification problems after a long absence, I find the probabilistic definitions intuitive and easy to recall. Additionally, whether we use precision-recall or sensitivity-specificity, there is a pleasing symmetry to both definitions. Precision determines the probability that a positive prediction belongs to the positive class, while recall gives the probability that a member of the positive class gets a positive prediction. That is, precision-recall deals exclusively with positive points and positive predictions, inverting what we condition on and what we predict for each metric. Sensitivity-specificity has its own symmetry—since sensitivity is the same as recall, and specificity gives the probability that a member of the negative class gets a negative prediction, we see that each metric is conditioned on the true labels for points, giving the probability that we make the correct prediction.

Two interesting properties of precision emerge from its probabilistic definition

By using a probabilistic definition of precision, we find two interesting properties by calling into service our good friend the Reverend Bayes. Precision is defined as

$$ p(y=1 | \hat{y}=1) = \frac{p(\hat{y}=1 | y=1) p(y=1)}{p(\hat{y}=1)} \ . $$

From this, we see that, unlike sensitivity and specificity, the true data distribution $p(y=1)$ enters into the definition of precision. Typically, we assume the classifier is trained on one dataset and thereafter remains static, such that its probability of making positive classifications $p(\hat{y}=1)$ is fixed. Conversely, the probability of the positive class $p(y=1)$ depends on the domain where the classifier is deployed—this probability may be similar to where the classifier was trained, or it may be substantially different.

Sensitivity and specificity should be independent of the dataset they’re used on, since they condition on the true labels. Precision, however, is not independent of the dataset on which it’s evaluated—it will increase as the population positive rate goes up. From this, we see that precision is equal to recall (sensitivity), weighted by the positive truth-to-label ratio $\frac{p(y=1)}{p(\hat{y}=1)}$. For a classifier to achieve good precision-recall, it must of course have good recall, while also ensuring that the number of points predicted as positive, reflected by $p(\hat{y}=1)$, does not grossly exceed the actual positives, reflected by $p(y=1)$. A classifier’s positive truth-to-label ratio may be good on one dataset, but on another dataset it may be poor—$p(\hat{y}=1)$ will remain constant, as it’s a property of the classifier, while $p(y)=1)$ can change, as it’s a property of the dataset Given this mismatch between the domain where a classifier is trained and where it is deployed, $\frac{p(y=1)}{p(\hat{y}=1)}$ may fall, causing the classifier’s precision to suffer.

Cheating your metrics

Consider our trifecta of precision, recall, and specificity. Given any two, we can always design a data distribution and a classifier such that the classifier performs well on our chosen two metrics, but poorly on the third. Alon Lekhtman did a fantastic job of considering all eight combinations of good and bad performance on these three metrics, and so I reuse his images here. The probabilistic perspective makes clear how to achieve the combination of good performance on two metrics and bad performance on one.

Bad precision, good sensitivity, good specificity. 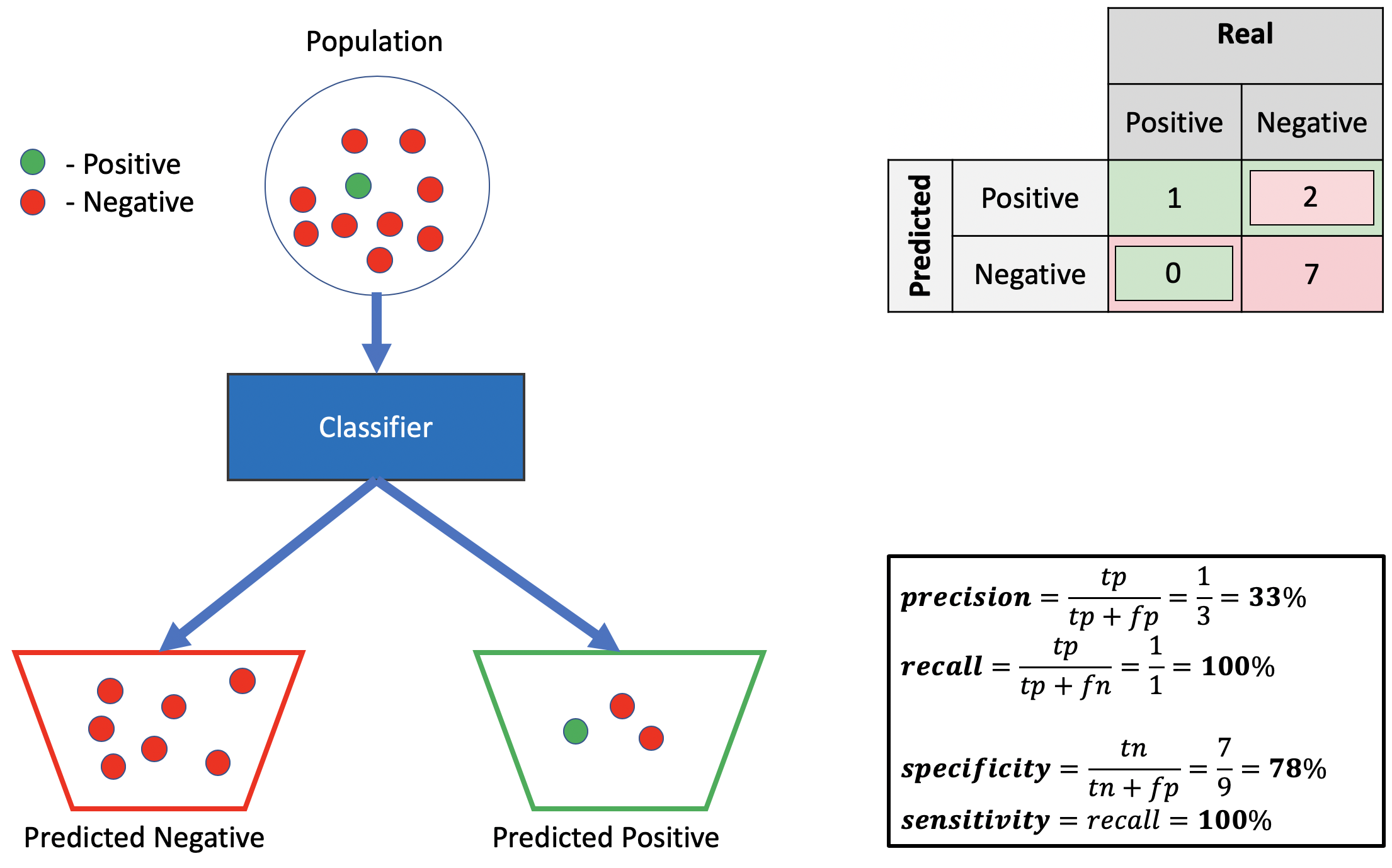Source: Alon Lekhtman

We achieve good sensitivity by correctly predicting all positives, and a good specificity by ensuring all predicted negatives are actually negative. Using the definition from the preceding section, we must have a low positive truth-to-label ratio to get poor precision, given our good sensitivity, which we accomplish by misclassifying two negative points as positive. Observe we can drive the precision as low as we wish by adding more such misclassified negative-predicted-as-positive points, without affecting recall or specificity.
Bad specificity, good precision, good recall. 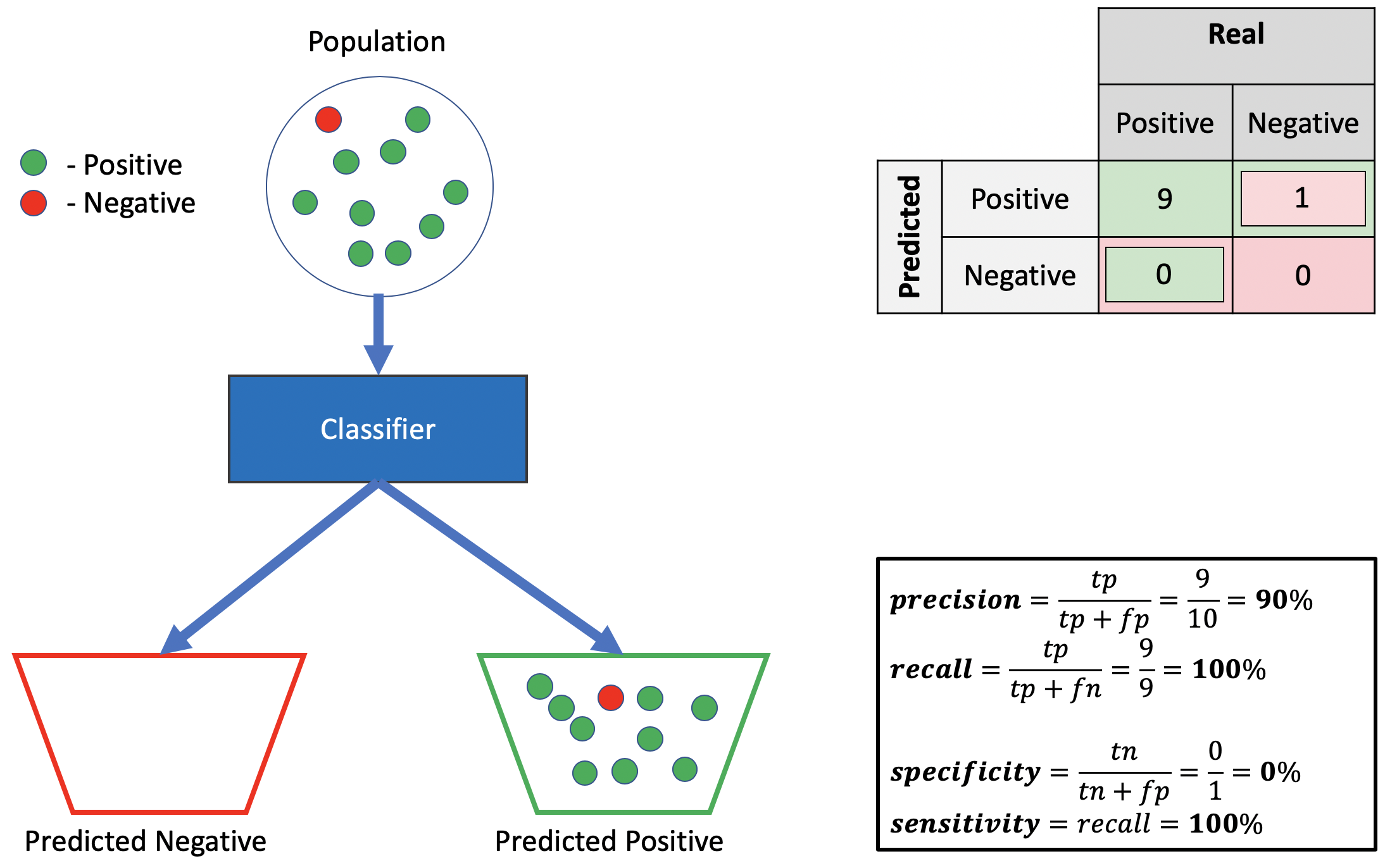Source: Alon Lekhtman

We achieve good recall by correctly classifying all positive points. Good precision follows by ensuring the positive truth-to-label ratio is high (i.e., $\frac{9}{10}$ of labelled positives are actually positive). Poor specificity requires $p(\hat{y}=0 | y=0)$ is low, implying $p(\hat{y}=1 | y=0)$ is high. This follows by mistakenly classifying all negative points as positive. Indeed, since neither precision nor recall draw on negative predictions, we need not classify anything as negative to achieve good performance.

Thus, neither precision-recall nor sensitivity-specificity alone are sufficient to characterize your classifier’s performance. To accurately evaluate performance using only two metrics, you must know what your data distribution will be.

If you know the distribution will be skewed such that it’s mostly negative, you should avoid sensitivity-specificity, since a classifier can achieve good performance in this scenario by assigning most points to the correct class, even though its positive predictions consist overwhelmingly of FPs. In this case, precision-recall is a better choice, since precision will heavily penalize a classifier whose positive truth-to-label ratio is low.
Conversely, if the distribution will be skewed to be mostly positive, you should avoid precision-recall, as simply predicting all points to be positive will result in the classifier doing well. Instead, you should use sensitivity-specificity, since specificity will penalize the classifier for having high $p(\hat{y}=1 | y=0)$.
Otherwise, if the distribution will be balanced with respect to positive and negative classes, either precision-recall or sensitivity-specificity should give you a reasonably accurate understanding of how your classifier is performing.

Better, however, is sidestepping the question of the true data distribution by simply using both metric pairs in unison.

Why does medicine prefer sensitivity-specificity to precision-recall?

Method evaluations in medicine often prefer sensitivity-specificity to precision-recall, perhaps because of the relative costs of FPs and FNs. In medical contexts, the cost of FNs can be much greater than FPs, especially when a test is widely deployed as a first-line screening measure. Consider a cancer screen examining elevated levels of prostate-specific antigen (PSA) in blood, which has a precision of only 25% but a sensitivity of 85%. A patient mistakenly classified as positive will undergo further tests that can recognize and correct this misclassification; conversely, a patient misclassified as negative could have his disease completely missed. Medical applications can thus tolerate a high FP rate, which corresponds to $p(y=0 | \hat{y}=1)$ being high, and implies the precision $p(y=1 | \hat{y}=1)$ can be low. Moreover, these applications typically occur in domains where the population positive rate $p(y=1)$ is low. Achieving good precision in such cases is difficult—you want to have good sensitivity, which requires being willing to classify a point as positive, even if you have only limited confidence in this choice. Good precision requires in concert that most points classified as positive are actually positive, which is hard; by contrast, good specificity requires only that most negative points are correctly assigned to the negative class, without any requirements about the relative balance between positive and negative points in the positive class. Cynically, then, medicine prefers specificity to precision simply because, in the setting where FNs are more costly than FPs, and where most tested points are negative, high precision is difficult to achieve while also not being critical for deployment.

In justifying medicine’s use of sensitivity-specificity in preference to precision-recall, we can also consider how these metrics are affected in the balance between positive and negative classes shifts between test development and deployment. Sensitivity and specificity are agnostic to the positive vs. negative class distribution, and so if a classifier exhibits good performance on these metrics during development using test data, it will likely continue to enjoy good sensitivity-specificity on real data, even if the distribution shifts between deployment sites or through time. Precision, conversely, depends on the population positive rate $p(y=1)$, and so good performance on this metric during development does not guarantee that performance will continue to be good should the distribution shift after deployment. Given the difficulty of revising a deployed test after gaining regulatory approval, we can suppose that the industry as a whole prefers metrics that are less sensitive to the true class distribution.

Other metric merits

Your metric preference can depend on factors beyond only the extent to which the metrics accurately convey your classifier’s performance in your domain. The ROC curve, which uses sensitivity-specificity, has three appealing properties relative to the precision-recall curve.

The ROC curve is monotonic, which serves as an easy diagnostic for erroneous curves. If your curve is not monotone, you know you’ve made an error in how you plot it. PR curves need not be monotonic.
A classifier that randomly guesses each point’s class will yield a diagonal line on the ROC curve. The area between your classifier’s curve and the diagonal thus gives an immediate illustration of how much better than random your classifier is.
The area under the ROC curve equals the probability that your classifier will rank a positive point above a negative one. This property reflects your classifier’s performance in a scale-invariant environment—it does not require that your classifier produce well-calibrated probability predictions, with the predicted positive probability reflecting what proportion of such predictions will be correct, or even that your classifier produce a probabilistic output at all. This can be a desirable or undesirable property, depending on whether you want to assess calibration.

Additionally, it’s worth noting that a classifier that dominates another in PR space will also do so in ROC space, and vice versa. This, however, tells you nothing about the absolute performance of the classifiers—both may in fact be quite bad.

Sometimes you have no choice

Finally, when choosing between sensitivity-specificity and precision-recall, observe that you may lack the concept of a TN. In such cases, you cannot use specificity, since it is defined as $p(\hat{y}=0 | y=0) = \frac{TN}{TN + FP}$. Precision and recall, however, do not require the concept of TNs, and so work fine given only TPs, FPs, and FNs.

This property was useful in the Pan-Cancer Analysis of Whole Genomes project, where, as part of an effort to assess the intratumor genetic heterogeneity for 2,658 cancers, we compared various algorithms for calling copy-number aberrations (CNA) on whole-genome sequencing data. To benchmark each of six algorithms, we conducted comparisons of each algorithm relative to a ground truth. Specifically, we were interested in how good algorithms were at determining genomic breakpoints where the copy-number status of a cancer genome changed. The question, then, was whether the candidate algorithm generally agreed with the ground-truth breakpoints. TPs were cases in which the candidate algorithm placed a breakpoint proximal to one in the ground truth (i.e., within 50 kb). FPs were candidate breakpoints placed without support from a proximal breakpoint in the ground truth. Finally, FNs were instances in which an algorithm did not place a proximal breakpoint relative to one in the ground truth. We had no concept of TN breakpoints, however, as this required somehow quantifying the notion that a region should have no breakpoints, and that none were placed. This would have required translating a concept dependent on the size of such breakpoint-free regions into integer counts, and so lacked the simple definition that we could establish for the other three confusion matrix classes. Lacking a coherent TN concept, we assessed performance via precision-recall, which did not require TNs, unlike sensitivity-specificity.

Previous post Next post