Introduction
A friend recently asked for my help in designing a computer science challenge for high school students as part of Let’s Talk Science, a non-profit that works to improve science literacy amongst grade-school students and educators. As part of this mission, Let’s Talk Science administers the SciEngTech Challenge, in which high school students participate in an all-day event that presents teams with science, engineering, math, and technology-based challenges. One challenge, for example, might present the team with a metre stick, then ask them to measure the height of a building. (This can be solved by using similar triangles to estimate the building’s height.) Time penalties are assessed based on how close the team’s answer was to the correct one, with the winning team being the one that completes all stations with the lowest overall completion time.
My task was simple: design a challenge that a team of six students could solve in 15 or 20 minutes. The challenge had to be designed such that it had a clear answer that could be objectively scored rather than judged. Though I could conceivably require that the team use computers to solve the problem, I wanted to avoid doing so, as computer science is often conflated with software engineering and programming by laypeople. Many of CS’s most beautiful ideas are entirely independent from the medium on which they’re expressed. In this regard, the computer bears the same relationship to CS that the telescope bears to astronomy–while an invaluable aid to exploring the applications and implications of the science, it is by no means necessary, and (at least in the case of CS) sometimes more a hindrance than a help.
One reasonably good challenge presents a sentence encoded with a Caesar cipher, then asks the students to decode it. The person running the station give a short explanation of what a Caesar cipher is, then leave the teams to decode a four- or five-word encoded phrase. Time penalties are awarded based on correctness, with each incorrect character adding a 30-second penalty. The Caesar cipher idea had been used often in the past, however, and I wished to develop something novel. I scrutinized the various activities on CS Unplugged, but none appealed to me–the exercises I saw were generally aimed at illustration of concepts and unsuitable for competition, were too simple, or required too much explanation of background knowledge.
The problem: Finding the minimum spanning tree
I eventually settled on a problem centred around determining the minimum spanning tree in a graph representing potential roads between Calgary communities. I phrased it thusly:
Pavement-eating termites have somehow chewed up every single road in Calgary, and so you must rebuild the road network from scratch. Your problem, however, is that the termites ate most of our money, too, and so you have only $42 billion at your disposal. You must figure out what combination of roads will let you travel between any two communities without exceeding this amount. (The cost for each potential road is listed next to it in the illustration.) You don’t need to build direct routes, however–for example, to go between Somerset and Tuscany, it’s perfectly acceptable to use the Somerset-Oakridge-Tuscany route.
I included this image to illustrate.
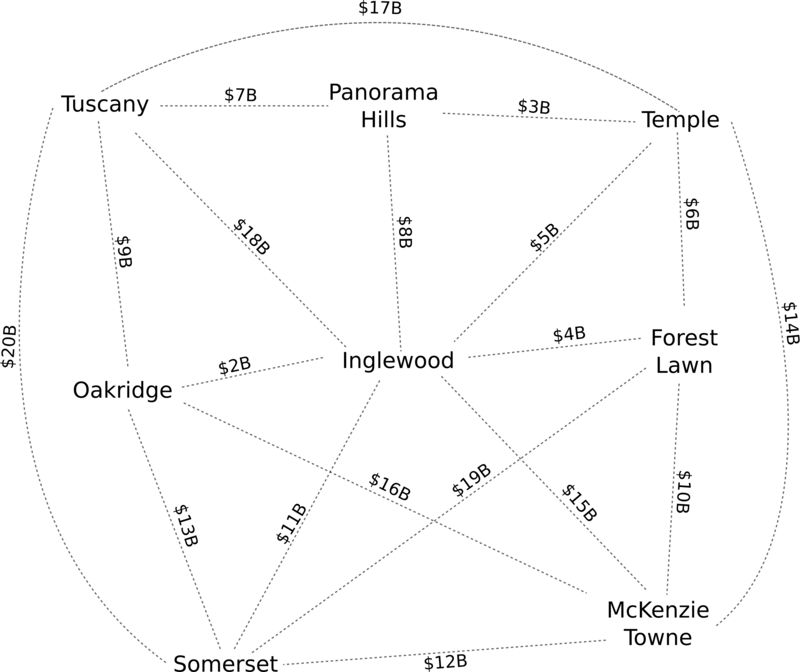
Several aspects of this problem appealed to me:
- It is easy to explain and understand, with the $42B cap serving as a self-evaluation that immediately reveals to students whether they’ve obtained the ideal answer.
- It lends itself to a trial-and-error approach driven by discussion, with the group ideally discovering that something such as Kruskal’s algorithm must yield the optimal answer.
- It has some appreciable connection to a real-world problem, contrived though may be the example’s formulation.
- It can be easily scored, with penalties assigned based on exceeding the $42B cap, or failing to connect all components of the graph.
More details, including the solution and a brief explanation of this problem’s connection to minimum spanning trees, Kruskal’s algorithm, and greedy algorithms in general, are available in my full write-up, available in PDF and Word formats.
Conclusion
The problem, alas, has not yet been put into practice. I look forward to seeing how it is received by students. Efforts such as this by Let’s Talk Science are wonderful, for they demonstrate to students that computer science’s purview extends well beyond writing iOS games and building web sites.